Question

For cones with radius 6 units, the equation =12ℎ V = 12 π h =12ℎ V = 12 π h relates the height ℎ h ℎ h of the cone, in units, and the volume V V of the cone, in cubic units.

Answer 1

Explanation:

The question is not properly structured. Here is the complete question.

For cones with radius 6 units, the equation V=12\pi h relates the height h of the cone, in units, and the volume V of the cone, in cubic units. Sketch a graph of this equation on the axes.

The formula for calculating the volume of a cone is expressed as shown;

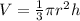`V = (1)/(3) \pi r^(2) h` where r is the radius and h is the height.

Given radius r = 6units, on substituting;

`V = (1)/(3)*\pi *6^(2)*h\\ V = (36\pi h)/(3)\\V = 12\pi h... (1)`

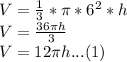
It can be seen from the derived volume of the cone that it is linear in nature. The volume of the cone has a linear relationship with its height. As the volume increases, the height also increases and vice versa.

Generally for a direct variation

`if\ y\ \alpha x \ \\y = kx`

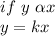
where k is the constant of proportionality. comparing to equation 1, k = 12π.

Find the graph attached