Answer:
A tree with a height of 6.2 ft is 3 standard deviations above the mean
Explanation:
⇒
 statement: A tree with a height of 5.4 ft is 1 standard deviation below the mean(FALSE)
statement: A tree with a height of 5.4 ft is 1 standard deviation below the mean(FALSE)
an X value is found Z standard deviations from the mean mu if:
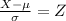
In this case we have:
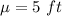

We have four different values of X and we must calculate the Z-score for each
For X =5.4\ ft
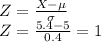
Therefore, A tree with a height of 5.4 ft is 1 standard deviation above the mean.
⇒
 statement:A tree with a height of 4.6 ft is 1 standard deviation above the mean. (FALSE)
statement:A tree with a height of 4.6 ft is 1 standard deviation above the mean. (FALSE)
For X =4.6 ft
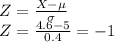
Therefore, a tree with a height of 4.6 ft is 1 standard deviation below the mean .
⇒
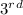 statement:A tree with a height of 5.8 ft is 2.5 standard deviations above the mean (FALSE)
statement:A tree with a height of 5.8 ft is 2.5 standard deviations above the mean (FALSE)
For X =5.8 ft
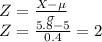
Therefore, a tree with a height of 5.8 ft is 2 standard deviation above the mean.
⇒
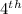 statement:A tree with a height of 6.2 ft is 3 standard deviations above the mean. (TRUE)
statement:A tree with a height of 6.2 ft is 3 standard deviations above the mean. (TRUE)
For X =6.2\ ft
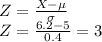
Therefore, a tree with a height of 6.2 ft is 3 standard deviations above the mean.