1 Answer

Dan Constantinescu · Answer 1 · 2021-05-31T22:52:44+0000

Answer:

The 90% confidence interval for the difference between means is (-161.18, 205.18).

Explanation:

Sample mean and standard deviation for Region I:

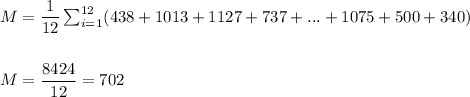
$M=(1)/(12)\sum_(i=1)^(12)(438+1013+1127+737+...+1075+500+340)\\\\\\ M=(8424)/(12)=702$

$s=\sqrt{(1)/((n-1))\sum_(i=1)^(12)(x_i-M)^2}\\\\\\s=\sqrt{(1)/(11)\cdot [(438-(702))^2+(1013-(702))^2+...+(500-(702))^2+(340-(702))^2]}\\\\\\$

$s=\sqrt{(1)/(11)\cdot [(69696)+(96721)+...+(131044)]}\\\\\\s=\sqrt{(1174834)/(11)}=√(106803.1)\\\\\\s=326.8$

Sample mean and standard deviation for Region II:

$M=(1)/(15)\sum_(i=1)^(15)(778+464+563+...+479+710+389+826)\\\\\\ M=(10204)/(15)=680$

$s=\sqrt{(1)/((n-1))\sum_(i=1)^(15)(x_i-M)^2}\\\\\\s=\sqrt{(1)/(14)\cdot [(778-(680))^2+(464-(680))^2+...+(389-(680))^2+(826-(680))^2]}\\\\\\$

$s=\sqrt{(1)/(14)\cdot [(9551.804)+(46771.271)+...+(84836.27)+(21238.2)]}\\\\\\ s=\sqrt{(545975.7)/(14)}=√(38998)\\\\\\s=197.5$

Now, we have to calculate a 90% confidence level for the difference of means.

The degrees of freedom are:

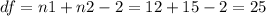
df=n1+n2-2=12+15-2=25

The critical value for 25 degrees of freedom and a confidence level of 90% is t=1.708

The difference between sample means is Md=22.

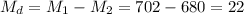
M_d=M_1-M_2=702-680=22

The estimated standard error of the difference between means is computed using the formula:

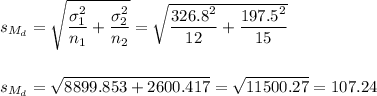
$s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}=\sqrt{(326.8^2)/(12)+(197.5^2)/(15)}\\\\\\s_(M_d)=√(8899.853+2600.417)=√(11500.27)=107.24$

The margin of error (MOE) can be calculated as:

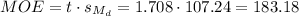
$MOE=t\cdot s_(M_d)=1.708 \cdot 107.24=183.18$

Then, the lower and upper bounds of the confidence interval are:

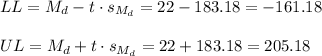
$LL=M_d-t \cdot s_(M_d) = 22-183.18=-161.18\\\\UL=M_d+t \cdot s_(M_d) = 22+183.18=205.18$

The 90% confidence interval for the difference between means is (-161.18, 205.18).

Please log in or register to add a comment.