Answer:
Option (b)
Explanation:
Let the points represented by the given table lie on a line.
And the equation of the line is,
y = mx + b
Where m = slope of the line
b = y-intercept
Let the points lying on the line are (0, -2) and (3, -3)
Slope of the line 'm' =
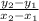
m =
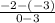
m =
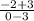
m = -

y-intercept 'b' = (-2)
Equation of the line is,
y =
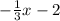
This equation matches with equation given in option (b).
Option (b) will be the answer.