Question

Particle A of charge 3.30 10-4 C is at the origin, particle B of charge -6.24 10-4 C is at (4.00 m, 0), and particle C of charge 1.06 10-4 C is at (0, 3.00 m). We wish to find the net electric force on C. (a) What is the x component of the electric force exerted by A on C?

Answer 1

a)
`E_T=134,484(N)/(C)\hat{i}+149954.66(N)/(C)\hat{j}`

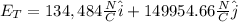
b) zero

Step-by-step explanation:

a) To find the electric field at point C, you sum the contribution of the electric fields generated by the other two charges. The total electric field at C is given by:

`E_T=E_1+E_2`

E1: electric field of charge 1

E2: electric field of charge 2

It is necessary to calculate the x and y components of both E1 and E2. You take into account the direction of the fields based on the charge q1 and q2:

`E_1=k(q_1)/(r_(1,3))[cos\theta\hat{i}+sin\theta \hat{j}]\\\\E_2=k(q_2)/(r_(2,3))[cos\phi\hat{i}-sin\phi \hat{j}]\\\\`

r13: distance between charges 1 and 3

r12: charge between charges 2 and 3

k: Coulomb's constant = 8.98*10^9 Nm^2/C^2

Thus, you first calculate the distance r13 and r23, and also the angles:

`r_(1,3)=3.00m\\\\r_(2,3)=√((3.00m)^2+(4.00m)^2)=5.00m\\\\\theta=90\°\\\\\phi=tan^(-1)((4.00)/(3.00))=53.13\°`

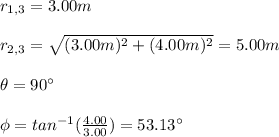
Next, you replace the values of all parameters in order to calculate E1 and E2:

`E_1=(8.98*10^9Nm^2/C^2)((3.30*10^(-4)C)/((3.00m)^2))\hat{j}\\\\E_1=329266.66(N)/(C)\\\\E_2=(8.98*10^9Nm^2/C^2)((6.24*10^(-4)C)/((5.00m)^2))[cos53.13\°\hat{i}-sin(53.13\°)\hat{j}]\\\\E_2=224140.8[0.6\hat{i}-0.8\hat{j}]=134484\hat{i}-179312\hat{j}`

finally, you obtain for ET:

`E_T=134,484(N)/(C)\hat{i}+(329266.66-179312)(N)/(C)\hat{j}\\\\E_T=134,484(N)/(C)\hat{i}+149954.66(N)/(C)\hat{j}`

b) The x component of the force exerted by A on C is zero because there is only a vertial distance between them. Thus, there is only a y component force.