Answer:
a)
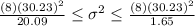
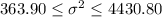
Now we just take square root on both sides of the interval and we got:
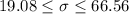
b) For this case we are 98% confidence that the true deviation for the population of interest is between 19.08 and 66.56
Explanation:
423.6, 487.3, 453.2, 402.9, 483.0, 477.7, 442.3, 418.4, 459.0
Part a
The confidence interval for the population variance is given by the following formula:

On this case we need to find the sample standard deviation with the following formula:
![s=sqrt{(\sum_(i=1)^8 (x_i -\bar x)^2)/(n-1)} </p><p>And in order to find the sample mean we just need to use this formula: </p><p>[tex]\bar x =(\sum_(i=1)^n x_i)/(n)]()
The sample deviation for this case is s=30.23
The next step would be calculate the critical values. First we need to calculate the degrees of freedom given by:
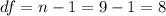
The Confidence interval is 0.98 or 98%, the value of
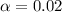 and
and
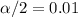 , and the critical values are:
, and the critical values are:
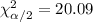
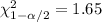
And replacing into the formula for the interval we got:
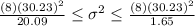
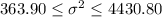
Now we just take square root on both sides of the interval and we got:
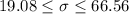
Part b
For this case we are 98% confidence that the true deviation for the population of interest is between 19.08 and 66.56