Question

The yearly amounts of carbon emissions from cars in Belgium are normally distributed with a mean of 13.9 gigagrams per year and a standard deviation of 5.8 gigagrams per year. Find the probability that the amount of carbon emissions from cars in Belgium for a randomly selected year are between 11.5 gigagrams and 14.0 gigagrams per year. a. 0.340 b. 0.660 c. 0.167 d. 0.397

Answer 1

The correct option is;

c. 0.167

Step-by-step explanation:

The parameters given are;

The mean, μ = 13.9 Gigagrams/year

The standard deviation, σ = 5.8 Gigagrams/year

The z-score formula is given as follows;

`z = (x - \mu )/(\sigma )`

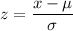
Where:

x = Observed score = 11.5 Gigagrams/year

We have;

`z = (11.5 - 13.9 )/(5.8 ) = (-2.4 )/(5.8 ) = 0.4138`

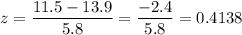
From the z-score table relations/computation, the probability (p-value) = 0.6605

Where:

x = Observed score = 14 Gigagrams/year

We have;

`z = (14- 13.9 )/(5.8 ) = (0.1)/(5.8 ) = 0.01724`

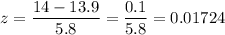
From the z-score table relations/computation, the probability (p-value) = 0.4931

Therefore, the probability,
`p_(ca)`, that the amount of carbon emissions from cars in Belgium for a randomly selected year are between 15.5 Gigagrams/year and 14 Gigagrams/year = The area under the normal curve bounded by the p-values for the two amounts of carbon emission

Which gives;

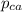`p_(ca)` = 0.6605 - 0.4931 = 0.1674 ≈ 0.167

Therefore, the correct option is c. 0.167.