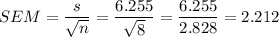Answer:
a. The mean of the sample is M=35.
The variance of the sample is s^2=39.125.
The standard deviation of the sample is s=6.255.
b. z=-1.6
c. SEM = 2.212
Step-by-step explanation:
The mean of the sample is M=35.
The variance of the sample is s^2=39.125.
The standard deviation of the sample is s=6.255.
Sample mean
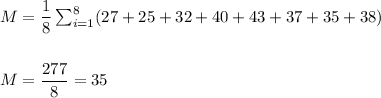
Sample variance and standard deviation
![s^2=(1)/((n-1))\sum_(i=1)^(8)(x_i-M)^2\\\\\\s^2=(1)/(7)\cdot [(27-(35))^2+(25-(35))^2+(32-(35))^2+(40-(35))^2+(43-(35))^2+(37-(35))^2+(35-(35))^2+(38-(35))^2]\\\\\\](https://img.qammunity.org/2021/formulas/mathematics/college/884r750zdvu3qrfi87fwbau6h6mljll0hu.png)
![s^2=(1)/(7)\cdot [(58.141)+(92.641)+(6.891)+(28.891)+(70.141)+(5.64)+(0.14)+(11.39)]\\\\\ s^2=(273.875)/(7)=39.125\\\\\\s=√(39.125)=6.255](https://img.qammunity.org/2021/formulas/mathematics/college/qmk1duyb0sw9rnksy9mdsm20s8becdnc4t.png)
b. If the population mean is 45, the z-score for M=35 would be:
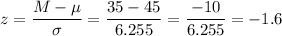
c. The standard error of the mean (SEM) of this group is calculated as: