Question

Two identical 82 mg dust particles very far apart (PEE 0) are moving directly toward each other at a speed of 3698 m/s. The charge on each is-719 ?C. Determine how close they will get to each other. Let k = 9x109 N-m2/C2 & ignore gravity.

Answer 1

r = 4.139

Step-by-step explanation:

In order to calculate how close the particles will get to each other, you take into account that all kinetic energy becomes electric potential energy between the particles when they are at the minimum distance. Then, you have:

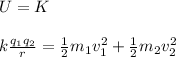`U=K\\\\k(q_1q_2)/(r)=(1)/(2)m_1v_1^2+(1)/(2)m_2v_2^2` (1)

q1 = q2: charge of the dust particles = -719μC = -719*10^-6 C

m1 = m2: mass = 82mg = 82*10^-6 kg

v1 = v2: speed of both particles = 3698 m/s

k: Coulomb's constant = 8.98*10^9 Nm^2/C^2

You solve the equation (1) for r:

`q_1=q_2=q\\\\m_1=m_2=m\\\\v_1=v_2=v\\\\k(q^2)/(r)=mv^2\\\\r=(kq^2)/(mv^2)`

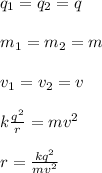
Finally, you replace the values of all parameters:

`r=((8.98*10^9Nm^2/C^2)(-719*10^(-6)C)^2)/((82*10^(-6)kg)(3698m/s)^2)\\\\r=4.139m`

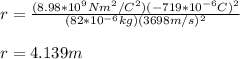
hence, the distance at which both dust particle are closer to each other is r = 4.139m