Question

A swimming pool with a volume of 30,000 liters originally contains water that is 0.01% chlorine (i.e. it contains 0.1 mL of chlorine per liter). Starting at t = 0, city water containing 0.001% chlorine (0.01 mL of chlorine per liter) is pumped into the pool at a rate of 20 liters/min. The pool water flows out at the same rate. Let A(t) represent the amount of chlorine (in mL) in the tank after t minutes. Write a differential equation for the rate at which the amount of chlorine in the pool is changing with respect to time. Then solve the DE to state a model representing the amount of chlorine in the pool at time t.

Be sure to remember to state the initial conditions for this DE clearly.
Rin =____________
Concentration of chlorine in the tank: c(t) =_________
Rout = _________
Differential equation:

Answer 1

`R_(in)=0.2(mL)/(min)`

`C(t)=(A(t))/(30000)`

`R_(out)= (A(t))/(1500) (mL)/(min)`

`A(t)=300+2700e^{-(t)/(1500)},$ A(0)=3000`

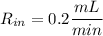
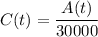
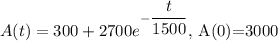
Explanation:

The volume of the swimming pool = 30,000 liters

(a) Amount of chlorine initially in the tank.

It originally contains water that is 0.01% chlorine.

0.01% of 30000=3000 mL of chlorine per liter

A(0)= 3000 mL of chlorine per liter

(b) Rate at which the chlorine is entering the pool.

City water containing 0.001%(0.01 mL of chlorine per liter) chlorine is pumped into the pool at a rate of 20 liters/min.

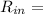`R_(in)=`(concentration of chlorine in inflow)(input rate of the water)

`=(0.01(mL)/(liter)) (20(liter)/(min))\\R_(in)=0.2(mL)/(min)`

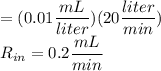
(c) Concentration of chlorine in the pool at time t

Volume of the pool =30,000 Liter

`Concentration, C(t)= (Amount)/(Volume)\\C(t)=(A(t))/(30000)`

(d) Rate at which the chlorine is leaving the pool

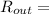`R_(out)=`(concentration of chlorine in outflow)(output rate of the water)

`= ((A(t))/(30000))(20(liter)/(min))\\R_(out)= (A(t))/(1500) (mL)/(min)`

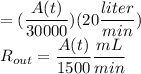
(e) Differential equation representing the rate at which the amount of sugar in the tank is changing at time t.

`(dA)/(dt)=R_(in)-R_(out)\\(dA)/(dt)=0.2- (A(t))/(1500)`

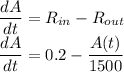
We then solve the resulting differential equation by separation of variables.

`(dA)/(dt)+(A)/(1500)=0.2\\$The integrating factor: e^{\int (1)/(1500)dt} =e^{(t)/(1500)}\\$Multiplying by the integrating factor all through\\(dA)/(dt)e^{(t)/(1500)}+(A)/(1500)e^{(t)/(1500)}=0.2e^{(t)/(1500)}\\(Ae^{(t)/(1500)})'=0.2e^{(t)/(1500)}`

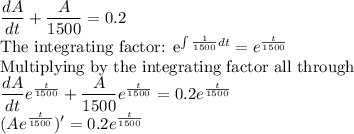
Taking the integral of both sides

`\int(Ae^{(t)/(1500)})'=\int 0.2e^{(t)/(1500)} dt\\Ae^{(t)/(1500)}=0.2*1500e^{(t)/(1500)}+C, $(C a constant of integration)\\Ae^{(t)/(1500)}=300e^{(t)/(1500)}+C\\$Divide all through by e^{(t)/(1500)}\\A(t)=300+Ce^{-(t)/(1500)}`

Recall that when t=0, A(t)=3000 (our initial condition)

`3000=300+Ce^(0)\\C=2700\\$Therefore:\\A(t)=300+2700e^{-(t)/(1500)}`