Question

The graph shows the solution for which inequalities?

Answer 1

Inequalities are,

y ≥ 4x + 2

y ≥ 2

Explanation:

Solid yellow line of the graph attached passes through two points (0, -2) and (1, 2).

Let the equation of this line is,

y = mx + b

Slope of the line =
`(y_(2)-y_(1))/(x_(2)-x_(1))`

m =
`(2+2)/(1-0)`

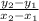
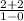
m = 4

Y-intercept 'b' = -2

Equation of the line will be,

y = 4x - 2

Since shaded area is on the left side of this solid line so the inequality representing this region will be,

y ≥ 4x - 2

Another line is a solid blue line parallel to the x-axis.

Shaded region (blue) above the line will be represented by,

y ≥ 2

Therefore, the common shaded area of these inequalities will be the solution of the given inequalities.