Question

Match each function with its domain. 1. S(x) = √x 2. H(x) = √2+x 3. Z(x) = √x-2 4. Q(x) = √2-x 5. V(x) = √-x 6. N(x) = ^3√2-x x ≤ 2 x ≥ -2 x ≥ 0 x ≥ 2 x ≤ 0 All real numbers

Answer 1

1. x ≥ 0

2. x ≥ -2

3. x ≥ 2

4. x ≤ 2

5. x ≤ 0

6. All real numbers

Explanation:

Domain of square function:

Suppose we have a square function in the following format:

`f(x) = \sqrt[n]{g(x)}`

If n is even, the domain of f(x) is:

`g(x) \geq 0`

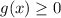
Otherwise, if n is odd, the domain of f(x) is all real numbers.

1. S(x) = √x

If n does not appear is that it is 2.

g(x) = x

So the domain is:

`x \geq 0`

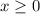
2. H(x) = √2+x

g(x) = 2 + x

So

`2 + x \geq 0`

`x \geq -2`

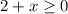
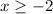
3. Z(x) = √x-2

g(x) = x - 2

`x - 2 \geq 0`

`x \geq 2`

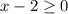
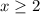
4. Q(x) = √2-x

g(x) = 2 - x

`2 - x \geq 0`

`-x \geq -2`

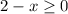
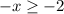
Multiplying by -1, everything

`x \leq 2`

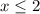
5. V(x) = √-x

g(x) = -x

Then

`-x \geq 0`

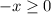
Multiplying by -1

`x \leq 0`

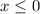
6. N(x) = ^3√2-x

Cubic root(odd number), so all real numbers.