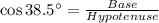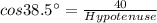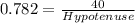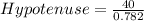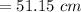Answer:
51.15 cm
Explanation:
Data provided
Basin = 40 centimeters deep
The Angle between the sloping sides = 77°
The calculation of the shortest distance between the tip of the cone and its rim is shown below:-
The angle will get divided and the angle is as follows
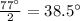
Here In the first triangle, we will follow "Cosine formula" which follows:-