Question

g In a certain​ lottery, an urn contains balls numbered 1 to 39 . From this​ urn, 5 balls are chosen​ randomly, without replacement. For a​ $1 bet, a player chooses one set of five numbers. To​ win, all five numbers must match those chosen from the urn. The order in which the balls are selected does not matter. What is the probability of winning this lottery with one​ ticket?

Answer 1

0.00017% probability of winning this lottery with one​ ticket

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

The order in which the balls are sorted is not important. So the combinations formula is used to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

What is the probability of winning this lottery with one​ ticket?

Desired outcomes:

One set, so
`D = 1`

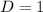
Total outcomes:

Five numbers, from a set of 39. So

`T = C_(39,5) = (39!)/(5!(39-5)!) = 575757`

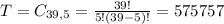
Probability:

`p = (D)/(T) = (1)/(575757) = 0.0000017`

0.00017% probability of winning this lottery with one​ ticket