Answer:
Asymptotic discontinuities at
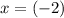 and
and
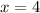 .
.
Explanation:
A linear function has an asymptotic discontinuity at
 if
if
 is a factor of the denominator after simplification.
is a factor of the denominator after simplification.
The numerator of this function,
 , is linear in
, is linear in
 .
.
The denominator of this function,
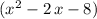 , is quadratic in
, is quadratic in
 . Using the quadratic formula or otherwise, factor the denominator into binominals:
. Using the quadratic formula or otherwise, factor the denominator into binominals:
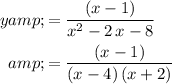 .
.
Simplify the function by liminating binomials that are in both the numerator and the denominator.
Notice that in the simplified expression, binomial factors of the denominator are
 and
and
 (which is equivalent to
(which is equivalent to
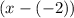 .) Therefore, the points of discontinuity of this function would be
.) Therefore, the points of discontinuity of this function would be
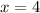 and
and
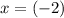 .
.