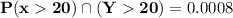Question

The future lifetimes (in months) of two components of a machine have the following joint density function: f(x, y) = {6/125,000 (50 - x - y) for 0 < x < 50 - y < 50, 0 otherwise. Write down a single integral representing the probability that both components are still functioning in 20 months from now.

Answer 1

Here is the correct computation of the question.

The future lifetimes (in months) of two components of a machine have the following joint density function:

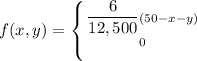`f(x,y) =\left \{ { {(6)/(12,500)(50-x-y)} \atop {0}} \right.` for 0 < x < 50 - y < 50, otherwise.

Write down a single integral representing the probability that both components are still functioning in 20 months from now.

Answer:

`\mathbf{ P{(x>20) \cap(Y>20)} } =0.0008}`

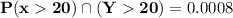
Explanation:

From the given information;

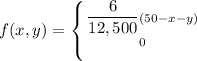`f(x,y) =\left \{ { {(6)/(12,500)(50-x-y)} \atop {0}} \right.` for 0 < x < 50 - y < 50, otherwise.

We can assert that the probability is the integral of the given density over the part of the range 0 ≤ x ≤ 50 - y ≤ 50 in which both x and y are greater than 20.

From the attached file below; their shows a probability density graph illustrating the above statement being said.

Now; to determine the probability that illustrates the integral of the density ; we have : P[(X > 20)∩(Y > 20)]

In addition to that:

From the image attached below;

We look into the region where the joint density under study is said to be positive and the triangle limits by the line axis x+y = 50

∴

`P{(x>20) \cap(Y>20)} } = (6)/(125000)\int\limits^(30)_(20)\int\limits^(50-x)_(20)(50-x-y)dydx`

`P{(x>20) \cap(Y>20)} } = (6)/(125000)\int\limits^(30)_(20) (1)/(2)(x-30^2)dx`

`P{(x>20) \cap(Y>20)} } = (6)/(125000) ( \, \frac {500}{3})`

`P{(x>20) \cap(Y>20)} } = (6*500)/(125000*3)`

`P{(x>20) \cap(Y>20)} } = (3000)/(375000)`

`\mathbf{ P{(x>20) \cap(Y>20)} } =0.0008}`

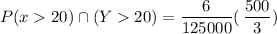
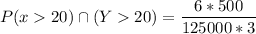
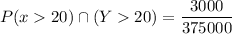
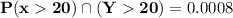
Thus; the single integral representing the probability that both components are still functioning in 20 months from now is
`\mathbf{ P{(x>20) \cap(Y>20)} } =0.0008}`