Answer:
The object hits the ground 5 seconds after being launched.
Explanation:
The height of the object in t seconds after being launched is given by the following equation:
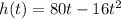
When will the object hit the ground after it is launched?
This is t for which h(t) = 0.
So
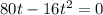
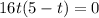
Then
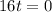
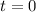
This is the launch point
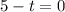
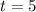
So
The object hits the ground 5 seconds after being launched.