Answer:
Reflect across the y-axis, stretch the graph vertically by a factor of 3, shift 2 units up.
Explanation:
The original function or the parent function is:
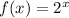
And the transformed function is:
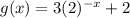
The transformations are as follows:
- Reflect the parent function about the y-axis, i.e. y : x → -x.
- Stretch the graph of the parent function vertically by 3 units, i.e.
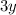
- Shift the graph, of the parent function, up by 2 units, i.e.
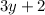 .
.
The transformed function is thus:
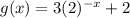 .
.
Thus, the correct option is:
"Reflect across the y-axis, stretch the graph vertically by a factor of 3, shift 2 units up."