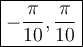Question

Verify that the indicated function y = f(x) is an explicit solution of the given first-order differential equation. Proceed as, by considering f simply as a function and give its domain. Then by considering f as a solution of the differential equation, give at least one interval I of definition.

y = 25 + y2; y = 5 tan 5x

Answer 1

Hence the domain of the function y = 5 tan 5x is ,

`\large \boxed {R-\{(2n+1)(\pi)/(10),n-1,2,...\} }`

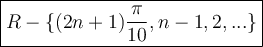
and largest interval of definition for the solution is
`\large \boxed {-(\pi)/(10),(\pi)/(10) }`

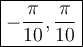
Explanation:

Considering the differential equation

`y' = 25 + y^2---(1)`

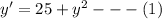
and the function y = 5 tan 5x

Find the domain of the function y = 5 tan 5x

Since
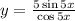`y=(5 \sin 5x)/(\cos 5x)` then determine the zeros of the denominator, cos 5x

The zeros of the denominator of cos 5x is
`\{ x:x=(2n+1)(\pi)/(10) \}`

Hence the function y = 5 tan 5x exist on
`R-\{(2n+1)(\pi)/(10) ,n=1,2...\}`

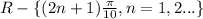
Therefore, the domain of the function y = 5 tan 5x is
`R-\{(2n+1)(\pi)/(10) ,n=1,2...\}`

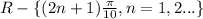
Differential the function y = 5 tan 5x with respect to x

`(d)/(dx) y=(d)/(dx) (5 \tan 5x)\\\\y'=5\sec^25x(d)/(dx) (5x)\\\\ \text {since }(d)/(du) (\tan u)= \sec^2 u\\\\y'=25 \sec^25x`

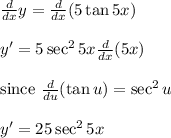
Use trigonometry identity ,
`1+\tan^2 \theta =\sec^2 \theta`

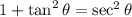
Substitute
`1+\tan ^25x\ \text{for} \sec^25x`

`y'=25(1+\tan^25x)\\y'=25+25\tan^25x\\y'=25+(5\tan5x)^2\\y'=25+y^2`

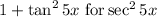
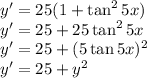
Therefore the function y = 5 tan 5x satisfies the differential equation
`y'=25+y^2`

Now , Find the largest interval of the solution

Since the tangent function is periodic with period π so take interval

`-(\pi)/(2) <5x<(\pi)/(2) \\\\-(\pi)/(10) <x<(\pi)/(10)`

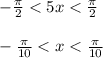
since , the function y = 5 tan 5x is not differentiatable at
`x = -(\pi)/(10)\ \text {and} \ x=(\pi)/(10)`

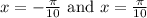
Hence the domain of the function y = 5 tan 5x is ,

`\large \boxed {R-\{(2n+1)(\pi)/(10),n-1,2,...\} }`

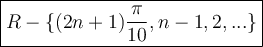
and largest interval of definition for the solution is
`\large \boxed {-(\pi)/(10),(\pi)/(10) }`