Question

Suppose we are interested in bidding on a piece of land and we know one other bidder is interested. The seller announced that the highest bid in excess of $10,000 will be accepted. Assume that the competitor's bid x is a is a random variable that is uniformly distributed between $10,000 and $15,000.

a. Suppose you bid $12,000. What is the probability that your bid will be accepted? (please show calculations)
b. Suppose you bid $14,000. What is the probability that your bid will be accepted? (please show calculations)
c. What amount should you bid to maximize the probability that you get the property? (please show calculations)d. Suppose you know someone who is willing to pay you $16,000 for the property. Would you consider bidding less than the amount in part (c)? Why or why not?

Answer 1

Explanation:

(a)

The bid should be greater than $10,000 to get accepted by the seller. Let bid x be a continuous random variable that is uniformly distributed between

$10,000 and $15,000

The interval of the accepted bidding is
`[ {\rm{\$ 10,000 , \$ 15,000}]`, where b = $15000 and a = $10000.

The interval of the provided bidding is [$10,000,$12,000]. The probability is calculated as,

`\begin{array}{c}\\P\left( {X{\rm{ < 12,000}}} \right){\rm{ = }}1 - P\left( {X > 12000} \right)\\\\ = 1 - \int\limits_(12000)^(15000) {\frac{1}{{15000 - 10000}}} dx\\\\ = 1 - \int\limits_(12000)^(15000) {\frac{1}{{5000}}} dx\\\\ = 1 - \frac{1}{{5000}}\left[ x \right]_(12000)^(15000)\\\end{array}`

`=1- ([15000-12000])/(5000)\\\\=1-0.6\\\\=0.4`

(b) The interval of the accepted bidding is [$10,000,$15,000], where b = $15,000 and a =$10,000. The interval of the given bidding is [$10,000,$14,000].

`\begin{array}{c}\\P\left( {X{\rm{ < 14,000}}} \right){\rm{ = }}1 - P\left( {X > 14000} \right)\\\\ = 1 - \int\limits_(14000)^(15000) {\frac{1}{{15000 - 10000}}} dx\\\\ = 1 - \int\limits_(14000)^(15000) {\frac{1}{{5000}}} dx\\\\ = 1 - \frac{1}{{5000}}\left[ x \right]_(14000)^(15000)\\\end{array} P(X<14,000)=1-P(X>14000)`

`=1- ([15000-14000])/(5000)\\\\=1-0.2\\\\=0.8`

(c)

The amount that the customer bid to maximize the probability that the customer is getting the property is calculated as,

The interval of the accepted bidding is [$10,000,$15,000],

where b = $15,000 and a = $10,000. The interval of the given bidding is [$10,000,$15,000].

`\begin{array}{c}\\f\left( {X = {\rm{15,000}}} \right){\rm{ = }}\frac{{{\rm{15000}} - {\rm{10000}}}}{{{\rm{15000}} - {\rm{10000}}}}\\\\{\rm{ = }}\frac{{{\rm{5000}}}}{{{\rm{5000}}}}\\\\{\rm{ = 1}}\\\end{array}`

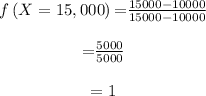
(d) The amount that the customer bid to maximize the probability that the customer is getting the property is $15,000, set by the seller. Another customer is willing to buy the property at $16,000.The bidding less than $16,000 getting considered as the minimum amount to get the property is $10,000.

The bidding amount less than $16,000 considered by the customers as the minimum amount to get the property is $10,000, and greater than $16,000 will depend on how useful the property is for the customer.