Answer:
The sum of the first 50 terms is 23825
Step-by-step explanation:
You posted this question in the wrong subject; This is mathematics not geography; However, the solution is as follows
Given
First Term: 11
32nd Term = 600
Required
Sum of first 50 terms
Using proper notations
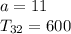
First the common difference has to be calculated;
The nth term of an arithmetic sequence is as follows
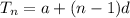
Where d represents the common difference
Using the data for
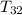 ; Substitute 11 for a and 32 for n
; Substitute 11 for a and 32 for n
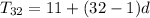
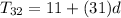
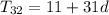
Recall that
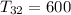
The above expression becomes
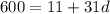
Subtract 11 from both sides
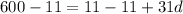
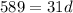
Divide both sides by 31
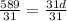
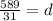
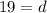
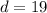
At this point the sum of first 50 terms can be calculates;
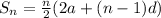
Substitute a = 11; n = 50 and d = 19
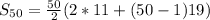
Start by solving the inner brackets
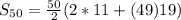
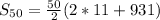
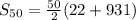

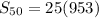
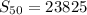
Hence, the sum of the first 50 terms is 23825