Question

A random sample of size nequals400 yielded ModifyingAbove p with caretequals0.35. a. Is the sample size large enough to use the large sample approximation to construct a confidence interval for​ p? Explain. b. Construct a 90​% confidence interval for p. c. Interpret the 90​% confidence interval. d. Explain what is meant by the phrase ​"90​% confidence​ interval."

Answer 1

a) i) np = 400*0.35=140 >10

ii) n(1-p)=400*(1-0.35) = 260>10

So then we can use the large sample approximation for this case

b)
`0.35 - 1.64 \sqrt{(0.35(1-0.35))/(400)}=0.311`

`0.35 + 1.64 \sqrt{(0.35(1-0.35))/(400)}=0.389`

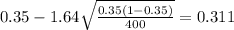
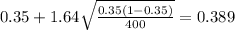
c) For this case we can conclude with a 90% of confidence that the true proportion of interest is between 0.311 and 0.389

d) For this case the 90% represent the confidence level for the proportion interval

Explanation:

Part a

We can check the assumption with these two rules:

i) np = 400*0.35=140 >10

ii) n(1-p)=400*(1-0.35) = 260>10

So then we can use the large sample approximation for this case

Part b

The confidence interval would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

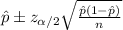
For the 90% confidence interval the value of
`\alpha=1-0.90=0.1` and
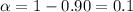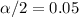`\alpha/2=0.05`, and the critical value would be

`z_(\alpha/2)=1.64`

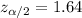
Replacing we got:

`0.35 - 1.64 \sqrt{(0.35(1-0.35))/(400)}=0.311`

`0.35 + 1.64 \sqrt{(0.35(1-0.35))/(400)}=0.389`

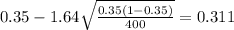
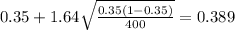
Part c

For this case we can conclude with a 90% of confidence that the true proportion of interest is between 0.311 and 0.389

Part d

For this case the 90% represent the confidence level for the proportion interval