Question

You are interested in finding a 90% confidence interval for the average commute that non-residential students have to their college. The data below show the number of commute miles for 11 randomly selected non-residential college students. Round answers to 3 decimal places where possible.

25 21 26 6 25 14 26 24 7 10 14
a. To compute the confidence interval use a distribution.
b. With 90% confidence the population mean commute for non-residential college students is between and miles.

Answer 1

a) 90 % of confidence interval is determined by

`(x^(-) -t_{(\alpha )/(2) } (S)/(√(n) ) , x^(-) +t_{(\alpha )/(2) } (S)/(√(n) ) )`

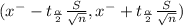
b) The 90% confidence intervals for the population mean

(13.6572 , 22.3428)

Explanation:

Step(i):-

Given data

Non residential college students 25 21 26 6 25 14 26 24 7 10 14

Mean of Non residential college students

x⁻ = ∑x/n

=
`(25+21+26+6+25+14+26+24+7+10+14)/(11)`

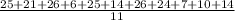
x⁻ = 18

now

Non residential

college students 'x' : 25 21 26 6 25 14 26 24 7 10 14

x - x⁻ : 7 3 8 -12 7 -4 8 6 -11 -8 -4

(x-x⁻)² : 49 9 64 144 49 16 64 36 121 64 16

`s^(2) = (49+9+64+144+49+16+64+36+121+64+16 )/(11-1)`

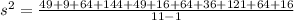
S² = 63.2

S = √63.2 = 7.949

Step(ii):-

The 90% confidence the population mean commute for non-residential college students is between and miles.

`(x^(-) -t_{(\alpha )/(2) } (S)/(√(n) ) , x^(-) +t_{(\alpha )/(2) } (S)/(√(n) ) )`

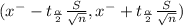
Degrees of freedom

ν =n-1 =11-1 = 10

t
`t_{(0.10)/(2) } = t_(0.05) = 1.812`

Step(iii):-

The 90% confidence the population mean commute for non-residential college students is between and miles.

`(x^(-) -t_{(\alpha )/(2) } (S)/(√(n) ) , x^(-) +t_{(\alpha )/(2) } (S)/(√(n) ) )`

`((18- 1.812 (7.949)/(√(11) ) , (18-+1.812 (7.949)/(√(11) ))`

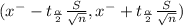
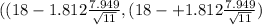
(18 - 4.3428 , 18 + 4.3428)

(13.6572 , 22.3428)

Conclusion:-

The 90% confidence the population mean commute for non-residential college students is between and miles.

(13.6572 , 22.3428)