Answer:
Odds to be given for an event that either Romance or Downhill wins is 11:4
Step-by-step explanation:
Given an odd, r = a : b. The probability of the odd, r can be determined by;
Pr(r) =
 ÷ (
÷ (
So that;
Odd that Romance will win = 2:3
Pr(R) =
 ÷ (
÷ (
=
 ÷
÷
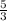
=
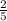
Odd that Downhill will win = 1:2
Pr(D) =
 ÷ (
÷ (
=
 ÷
÷

=

The probability that either Romance or Downhill will win is;
Pr(R) + Pr(D) =
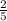 +
+

=
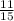
The probability that neither Romance nor Downhill will win is;
Pr(neither R nor D) = (1 -
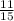 )
)
=
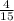
The odds to be given for an event that either Romance or Downhill wins can be determined by;
= Pr(Pr(R) + Pr(D)) ÷ Pr(neither R nor D)
=
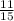 ÷
÷
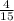
=
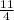
Therefore, odds to be given for an event that either Romance or Downhill wins is 11:4