Question

Prove the trig identity: tan^2 x cos^2 x = (sec^2 x -1)(1-sin^4 x)/1+sin^2 x

Answer 1

See steps below

Explanation:

We need to work with each side of the equation at a time:

Left hand side:

Write all factors using the basic trig functions "sin" and "cos" exclusively:

`tan^2(x)\,cos^2(x)=(sin^2(x))/(cos^2(x)) cos^2(x)=sin^2(x)`

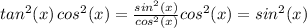
now, let's work on the right side, having in mind the following identities:

a)
`sec^2(x)-1=tan^2(x)=(sin^2(x))/(cos^2(x))`

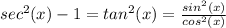
b)
`1-sin^4(x) =(1-sin^2(x))\,(1+sin^2(x))`

c)
`1-sin^2(x)=cos^2(x)`

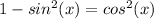
Then replacing we get:

`((sec^2(x)-1)\,(1-sin^4(x)))/(1+sin^2(x)) =(sin^2(x)(1+sin^2(x))(1-sin^2(x)))/(cos^2(x)(1+sin^2(x)))) =(sin^2(x)(1+sin^2(x))\,cos^2(x))/(cos^2(x)(1+sin^2(x))))=sin^2(x)`

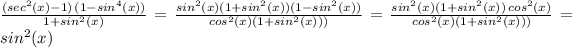
Therefore, we have proved that the two expressions are equal.