Question

An ideal diatomic gas undergoes a cyclic process. In the first step, the gas undergoes an isothermal expansion from V1 to 3.00 V1. In the second step of the process the gas undergoes an isovolumetric decrease in pressure. In the third step the gas undergoes an adiabatic compression from 3.00 V1 back to V1 completing the cycle.

Required:
a. Sketch the cycle.
b. In terms of P., V. and T., determine P2, P3, T3.
c. In terms of P., V. To determine W, Q and ΔE int for each step. Take T, to be between 100K and 1000K

Answer 1

Step 1

Work done = -9134.4 J

ΔQ = -9134.4 J

Step 2

ΔQ = -3570.32 J = ΔU

W = 0

Step 3

The pdV work done = 3570.32 J

The Vdp work done = 11053.37 J

Heat transferred, ΔE = 0.

Step-by-step explanation:

For diatomic gases γ = 1.4

Step 1

Where:

v₂ = 3.00·v₁

On isothermal expansion of an ideal gas by Boyle's law, we have;

p₁·v₁ = p₂·v₂ which gives;

p₁·v₁ = p₂×3·v₁

Dividing both sides by v₁, we have;

p₁= 3·p₂

`p_2 = (p_1)/(3)`

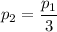
Hence, the pressure is reduced by a factor of 3

Work done =

`n\cdot R\cdot T\cdot ln(v_(f))/(v_(i))`

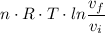
Where:

n = 1 mole

R = 8.3145 J/(mole·K)

T = 1000 K we have

`1 * 8.3145 * 1000 * ln\left ((1)/(3) \right ) = -9134.4 J`

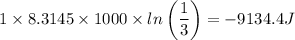
Step 2

The gas undergoes a constant volume decrease in pressure given by Charles law as follows;

`(p_2)/(p3) = (T_1)/(T_3)`

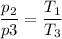
Whereby p₂ > p₃, T₁ will be larger than T₃

W = 0 for constant volume process

ΔQ = m×cv×ΔT = 1 × 3.97 × -900 = -3570.32 J = ΔU

Step 3

For adiabatic compression, we have;

`(p_3)/(p_1) = \left ((V_1)/(V_3) \right )^(\gamma ) = \left ((T_3)/(T_1) \right )^{(\gamma )/(\gamma -1)}`

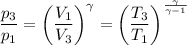
Where:

T₁ = 1000 K

T₃ = 100 K

We have;

`\left ((V_1)/(3\cdot V_1) \right )^(\gamma ) = \left ((100)/(1000) \right )^{(\gamma)/(\gamma -1)}`

`\left ((1)/(3) \right ) = \left ((1)/(10) \right )^{(1)/(\gamma -1)}`

`log\left ((1)/(3) \right ) = {(1)/(\gamma -1)} * log \left ((1)/(10) \right )^`

`\gamma -1 =(log \left ((1)/(10) \right ))/( log\left ((1)/(3) \right ) ) {`

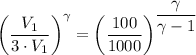
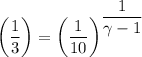
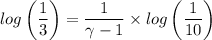
∴ γ-1 = 2.096

γ = 3.096

The pdV work done =

`m * c_v * (T_1 - T_3)`

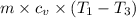
m×R/(γ - 1)×(T₁ - T₃) =

3.97×(1000 - 100) = 3570.32 J

The Vdp work done =

`m * c_p * (T_1 - T_3)`

`c_p = k * c_v = 3.096 * 3.97 = 12.3 \, J/(mol\cdot K)`

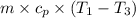
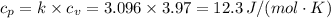
12.3×(1000 - 100) = 11053.37 J

Heat transferred, ΔE = 0.