Answer:
The value of the Riemann sum is 200.
Explanation:
Let the region bounded by the trapezoid is shown as attached figure. Thus the different regions are formed for which the centroid points are calculated as follows
R-1 is the region formed as right angle triangle between points (x1,y1)=(0,0), (x2,y2)=(2,0) and (x3,y3)=(2,2). The centroid is given as
Centroid for this region is given as
C-R1 is (x1+x2+x3)/3,(y1+y2+y3)/3 which is (0+2+2)/3, (0+0+2)/3 given as ()
Similary the Centroids of other regions are given as
C-R2=(10/3,8/3), C-R3=(3,1), C-R4=(5,3), C-R5=(5,1), C-R6=(7,3), C-R7=(7,1),
C-R8=(26/3,8/3), C-R9=(9,1) and C-R10=(32/3,2/3)
Now using the following equation, the Riemann sum is given as
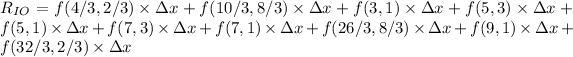 Here value of f is simple product of the points and the value of Δx is 2. Plugging in the values give the value of Riemann Sum as
Here value of f is simple product of the points and the value of Δx is 2. Plugging in the values give the value of Riemann Sum as
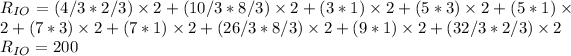
So the value of the Riemann sum is 200.