Question

A 74.0 kg tightrope walker stands at the center of a rope. The rope supports are 10 m apart and the rope sags 8.00 ∘ at each end. The tightrope walker crouches down, then leaps straight up with an acceleration of 7.80 m/s2 to catch a passing trapeze.

Required:
What is the tension in the rope as he jumps?

Answer 1

285.79 N

Step-by-step explanation:

Mass m of tightrope walker = 74.0 kg

distance of both ends pf rope = 10 m

angle at both ends of the rope = 8.00°

acceleration a of leap = 7.80
`m/s^(2)`

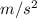
Force exerted on the rope due to the acceleration will be,

F = ma

F = 74 x 7.80 = 577.2 N

This force creates a tension that is evenly divided on the ropes from the midpoint, i.e force on each end of the rope = 288.6 N

Tension T = F sin∅

T = 288.6 sin 8.00° = 285.79 N