Question

Ned's Natural Foods sells unshelled peanuts by the pound Historically, Ned has observed that daily demand is normally distributed with a mean of 80 pounds and a standard deviation of 10 pounds Lead time also appears normally distributed with a mean of eight days and a standard deviation of one day. Use Table What ROP would provide a stock out risk of 10 percent during lead time? (Round your answer to the nearest whole number.) rope units What is the expected number of units (pounds) short per cycle? (Round your answer to 3 decimal places.) Expected number of units

Answer 1

a) 749

b) 4.073

Step-by-step explanation:

Given:

Mean = demand = 80 pounds

Standard deviation of demand = 10 pounds

Lead time = 8 days

Standard deviation of lead time = 1 day

a) What ROP would provide a stock out risk of 10 percent during lead time.

To find this re-order point (ROP) quantity, take the formula:

`ROP = d(LT) + z √( LT \sigma_d ^2 + LT^2 \sigma_L_T ^2)`

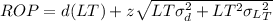
Here, service level = 100%-10% = 90%,

Thus z at 90% = ±1.28

`ROP = 80(8) + 1.28 √(8* 10^2 + (8)^2*(1)^2)`

`ROP = 640 + 1.28√(800 + 64)`

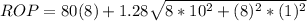
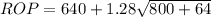
= 640 + 1.28* 84.85

= 748.61

≈ 749 units

b) What is the expected number of units (pounds) short per cycle.

Find the number of units shorts per cycle. Take the formula:

`E(n) = E(z) * \sigma d_L_T`

[

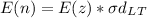
Where E(z) = standardized number of shorts = 0.048

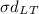`\sigma d_L_T` = standard deviation of lead time demand = 84.85

Therefore,

E(n) = 0.048 * 84.85

= 4.073