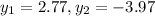Question

Find the intersection(s) of the line y = 2x - 3 with the circle whose center at origin, radius = 4

Answer 1

`x = (12 \pm √((-12)^2 -4(5)(-7)))/(2(5))`

And we got for the solution:

`x_1= 2.885 , x_2 = -0.485`

And the value sof y are using the function y =2x-3:

`y_1=2.77, y_2=-3.97`

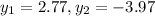
Explanation:

For this case we have this function given:

`y = 2x-3` (1)

And the circle with center the origin and radius 4 is given by;

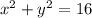`x^2 +y^2 = 16` (2)

We can solve fro y from the last equation and we got:

`y = \pm √(16-x^2)` (3)

Now we can set equal equations (3) and (1) and we got:

`2x-3 = √(16-x^2)`

`(2x-3)^2=16-x^2`

`4x^2 -12x +9 = 16-x^2`

`5x^2 -12x -7=0`

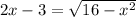
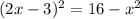
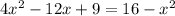
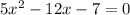
And using the quadratic equation we got:

`x = (12 \pm √((-12)^2 -4(5)(-7)))/(2(5))`

And we got for the solution:

`x_1= 2.885 , x_2 = -0.485`

And the value sof y are using the function y =2x-3:

`y_1=2.77, y_2=-3.97`