Question

Use the given inverse to solve the system of equations. left brace Start 3 By 3 Matrix 1st Row 1st Column x minus y plus z 2nd Column equals 3rd Column negative 6 2nd Row 1st Column 2 y plus z 2nd Column equals 3rd Column negative 6 3rd Row 1st Column 3 x minus 8 y 2nd Column equals 3rd Column negative one half EndMatrix The inverse of left bracket Start 3 By 3 Matrix 1st Row 1st Column 1 2nd Column negative 1 3rd Column 1 2nd Row 1st Column 0 2nd Column 2 3rd Column 1 3rd Row 1st Column 3 2nd Column negative 8 3rd Column 0 EndMatrix right bracket is left bracket Start 3 By 3 Matrix 1st Row 1st Column negative 8 2nd Column 8 3rd Column 3 2nd Row 1st Column negative3 2nd Column 3 3rd Column 1 3rd Row 1st Column 6 2nd Column negative 5 3rd Column negative 2 EndMatrix right bracket .

Answer 1

The interpretation of the given question is as follows:

Use the given inverse to solve the system of equations

`x- y - z = -6 \\ \\ 2y + z = -6 \\ \\ 3x -8 y = - (1)/(2)`

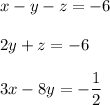
The inverse of
`\left[\begin{array}{ccc}1&-1&1\\0&2&1\\3&-8&0\end{array}\right] is \left[\begin{array}{ccc}-8&8&3\\-3&3&1\\6&-5&-2\end{array}\right]`

x =

y =

z =

Answer:

x = - 1.5

y = - 0.5

z = - 5

Explanation:

Using the correlation of inverse of matrix AX = B to solve the question above;

AX = B

⇒ A⁻¹(AX) = A⁻¹ B

X = A⁻¹ B

So ;

X = A⁻¹ B

`\left[\begin{array}{c}x\\y\\z\end{array}\right] =`
`\left[\begin{array}{ccc}-8&8&3\\-3&3&1\\6&-5&-2\end{array}\right] =`
`\left[\begin{array}{ccc}-6\\ -6\\- (1)/(2)\end{array}\right]`

`\left[\begin{array}{c}x\\y\\z\end{array}\right] =\left[\begin{array}{ccc}(-8*-6)+(8*-6)+(3*-(1)/(2))\\(-3*-6)+(3*-6)+(1*-(1)/(2))\\(6*-6)+(5*-6)+(-2* - (1)/(2))\end{array}\right]`

`\left[\begin{array}{c}x\\y\\z\end{array}\right] =\left[\begin{array}{ccc}(48)+(-48)+((-3)/(2))\\(18)+(-18)+((-1)/(2))\\(-36)+(30)+(1)\end{array}\right]`

`\left[\begin{array}{c}x\\y\\z\end{array}\right] =\left[\begin{array}{ccc}((-3)/(2))\\((-1)/(2))\\(-5)\end{array}\right]`

`\left[\begin{array}{c}x\\y\\z\end{array}\right] =\left[\begin{array}{ccc}-1.5\\-0.5\\ -5\end{array}\right]`