Answer:
By Side-Side-Side (SSS) property, CA = CB
Explanation:
Given: /AB/ and bisector /CD/.
Proof: CA = CB
But,
AD = BD (since D is the midpoint of AB)
<CDA = CDB (right angle property)
<CAD = CBA (congruent property of triangles)
Therefore;
Δ ACD = ΔBCD (congruence property)
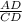 =
=
 (proportion of the sides of two congruent triangles)
(proportion of the sides of two congruent triangles)
Thus, by Side-Side-Side (SSS) property, CA = CB