Question

Find the number of positive integers less than 100,000 whose digits are among 1, 2, 3, and 4. Hint consider the

possibilities for 5-digit, 4-digit, 3-digit, 2-digit, and 1-digit numbers and repetition of digits.

Answer 1

This is a waste of time. I'm sorry you have to do this, this is pointless. I did it too. I'll spare you the calculations — it's 1364.

Answer 2

1364 is the number of possibilities for positive integers less than 1,00,000.

Explanation:

1. 5 digit numbers:

We have 5 places here, and each place can have 4 options because repetition is allowed.

So, total number of possibilities for 5 digit numbers:

`4 * 4 * 4 * 4 * 4\\ \Rightarrow 1024`

2. 4 digit numbers:

We have 4 places here, and each place can have 4 options because repetition is allowed.

So, total number of possibilities for 4 digit numbers:

`4 * 4 * 4 * 4 \\ \Rightarrow 256`

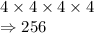
3. 3 digit numbers:

We have 3 places here, and each place can have 4 options because repetition is allowed.

So, total number of possibilities for 3 digit numbers:

`4 * 4 * 4 \\ \Rightarrow 64`

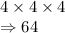
4. 2 digit numbers:

We have 2 places here, and each place can have 4 options because repetition is allowed.

So, total number of possibilities for 2 digit numbers:

`4 * 4 \\ \Rightarrow 16`

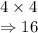
5. 1 digit numbers:

We have 1 place here, and each place can have 4 options because repetition is allowed.

So, total number of possibilities for 1 digit numbers:

`4`

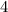
We can add all the above possibilities to find the total.

So, number of positive integers less than 100,000 whose digits are among 1, 2, 3, and 4 = 1024 + 256 + 64 + 16 + 4 = 1364