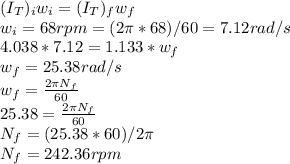Question

On average, both arms and hands together account for 13% of a person's mass, while the head is 7.0% and the trunk and legs account for 80%. We can model a spinning skater with her arms outstretched as a vertical cylinder (head, trunk, and legs) with two solid uniform rods (arms and hands) extended horizontally. Suppose a 74.0 kg skater is 1.80 m tall, has arms that are each 70.0 cm long (including the hands), and a trunk that can be modeled as being 35.0 cm in diameter. If the skater is initially spinning at 68.0 rpm with her arms outstretched, what will her angular velocity 2 be (in rpm ) after she pulls in her arms and they are at her sides parallel to her trunk? Assume that friction between the skater and the ice is negligble.

Answer 1

Angular velocity,
`N_f = 242.36 rpm`

Step-by-step explanation:

The mass of the skater, M = 74.0 kg

Mass of each arm,
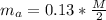`m_(a) = 0.13 * (M)/(2)` ( since it is 13% of the whole body and each arm is considered)

`m_(a) = 0.13 * 37\\m_a = 4.81 kg`

Mass of the trunk,
`m_(t) = M - 2m_(a)`

`m_t = 74 - 2(4.81)\\m_(t) = 64.38 kg`

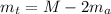
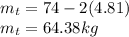
Total moment of Inertia = (Moment of inertia of the arms) + (Moment of inertia of the trunks)

`(I_(T) )_i = 2((m_(a)L^2 )/(12) + m_a(0.5L + R)^2) + 0.5 m_t R^2`

`(I_(T) )_i = 2((4.81 * 0.7^2 )/(12) + 4.81(0.5*0.7 + 0.175)^2) + 0.5 *64.38* 0.175^2\\(I_(T) )_i = 3.052 + 0.986\\(I_(T) )_i = 4.038 kgm^2`

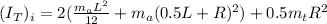
The final moment of inertia of the person:

`(I_(T) )_f = (1)/(2) MR^(2) \\(I_(T) )_f = (1)/(2) * 74*0.175^(2)\\(I_(T) )_f = 1.133 kg.m^2`

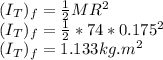
According to the principle of conservation of angular momentum:

`(I_(T) )_i w_(i) = (I_(T) )_f w_(f)\\w_(i) = 68 rpm = (2\pi * 68)/60 = 7.12 rad/s\\4.038 * 7.12 =1.133* w_(f)\\w_(f) = 25.38 rad/s\\w_(f) = (2\pi N_f)/(60) \\25.38 = (2\pi N_f)/(60)\\N_f = (25.38 * 60)/2\pi \\N_f = 242.36 rpm`