Question

Two non-conducting slabs of infinite area are given a charge-per-unit area of σ = -16 C/m^2 and σb =+6.0 C/m^2 respectively. A third slab, made of metal, is placed between the first two plates. The charge density σm on the metal slab is 0 (i.e., the slab is uncharged).

Required:
Find the magnitude and direction of the electric field.

Answer 1

`E_(C) = -5.65 * 10^(11) \hat{x}` N/C

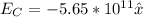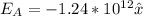`E_(A) = -1.24 * 10^(12) \hat{x}` N/C

Step-by-step explanation:

The charge per unit area of the two non-conducting slabs are given by:

`\sigma_(a) = -16 C/m^2`

`\sigma_(b) = 6 C/m^2`

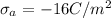
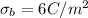
The charge density on the metal
`\sigma_(m) = 0`

ε0 = 8.854 x 10-12 C2/N m2

Note that the electric field inside the conductor is zero because it is an equipotential surface.

The diagram attached to this solution typifies the description given in the question:

The electric field in the region C can be calculated by:

`E_(C) = ( |\sigma_(b) |- |\sigma_(a)| )/(2 \epsilon_(0) ) \\E_(C) = (6 - 16 )/(2 * 8.854 * 10^(-12) ) \\E_(C) = -5.65 * 10^(11) \hat{x}`

The electric field in the region A can be calculated by:

`E_(A) = (- |\sigma_(a) |- |\sigma_(b)| )/(2 \epsilon_(0) ) \\E_(A) = (-16 - 6 )/(2 * 8.854 * 10^(-12) ) \\E_(A) = -1.24 * 10^(12) \hat{x}`