Answer:
(a) Probability that Y falls into the dangerous region is 0.0013.
(b) Probability that the mean Y-bar falls into the dangerous region is 0.00001.
Explanation:
We are given that a certain capsule is manufactured so that the dosage of the active ingredient follows the distribution Y ~ N(μ = 10 mg, σ = 1 mg).
A dosage of 13 mg is considered dangerous.
Let Y = dosage of the active ingredient
The z-score probability distribution for normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean = 10 mg
= population mean = 10 mg
 = standard deviation = 1 mg
= standard deviation = 1 mg
(a) Probability that Y falls into the dangerous region is given by = P(Y
 13 mg)
13 mg)
P(Y
 13 mg) = P(
13 mg) = P(


 ) = P(Z
) = P(Z
 3) = 1 - P(Z < 3)
3) = 1 - P(Z < 3)
= 1 - 0.9987 = 0.0013
The above probability is calculated by looking at the value of x = 3 in the z table which has an area of 0.9987.
(b) We are given that a dosage of 13 mg is considered dangerous. And we sample 49 capsules at random.
Let
 = sample mean dosage
= sample mean dosage
The z-score probability distribution for sample mean is given by;
Z =
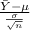 ~ N(0,1)
~ N(0,1)
where,
 = population mean = 10 mg
= population mean = 10 mg
 = standard deviation = 1 mg
= standard deviation = 1 mg
n = sample of capsules = 49
So, Probability that the mean Y-bar falls into the dangerous region is given by = P(

 13 mg)
13 mg)
P(Y
 13 mg) = P(
13 mg) = P(
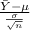

 ) = P(Z
) = P(Z
 21) = 1 - P(Z < 21)
21) = 1 - P(Z < 21)
= 0.00001