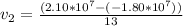Question

You are at the controls of a particle accelerator, sending a beam of 2.10×107 m/s protons (mass m) at a gas target of an unknown element. Your detector tells you that some protons bounce straight back after a collision with one of the nuclei of the unknown element. All such protons rebound with a speed of 1.80×107 m/s. Assume that the initial speed of the target nucleus is negligible and the collision is elastic.

A) Find the mass of one nucleus of the unknown element.
B) What is the speed of the unknown nucleus immediately after such a collision?

Answer 1

a

The mass is
`m_2 =21.75*10^(-27) \ kg`

b

The velocity is
`v_2 = 3.0*10^(6) m/s`

Step-by-step explanation:

From the question we are told that

The speed of the protons is
`u_1 = 2.10*10^(7) m/s`

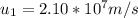
The mass of the protons is
`m`

The speed of the rebounding protons are
`v_1 = -1.80 * 10^(7) \ m/s`

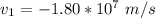
The negative sign shows that it is moving in the opposite direction

Now according to the law of energy conservation mass of one nucleus of the unknown element. is mathematically represented as

`m_2 = [(u_1 -v_1)/(u_1 + v_1) ] m_1`

Where
`m_1` is the mass of a single proton

So substituting values

`m_2 = \frac{2.10 *10^(7) - (-1.80 *10^(7))} {(2.10 *10^7) + (-1.80 *10^(7))} m_1`

`m_2 =13 m_1`

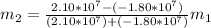
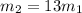
The mass of on proton is
`m_1 = 1.673 * 10^(-27) \ kg`

So
`m_2 =13 ( 1.673 * 10^(-27) )`

`m_2 =21.75*10^(-27) \ kg`

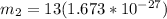
Now according to the law of linear momentum conservation the speed of the unknown nucleus immediately after such a collision is mathematically evaluated as

`m_1 u_1 + m_2u_2 = m_1 v_1 + m_2v_2`

Now
`u_2` because before collision the the nucleus was at rest

So

`m_1 u_1 = m_1 v_1 + m_2v_2`

=>
`v_2 = (m_1(u_1 -v_1))/(m_2)`

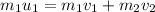
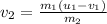
Recall that
`m_2 =13 m_1`

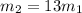
So

`v_2 = (m_1(u_1 -v_1))/(13m_1)`

=>
`v_2 = ((u_1 -v_1))/(13)`

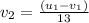
substituting values

`v_2 = (( 2.10*10^(7) -(-1.80 *10^(7))))/(13)`

`v_2 = 3.0*10^(6) m/s`