Answer:
The correct option is |(45) = $41.54, P(45) = $319.52
Step-by-step explanation:
Loan amount = Price - Down payment = $25499 - $3240 = $22259
Monthly interest rate = i = 5.25%÷ 12 = 0.004375
Number of installments = n =72
Monthly installment=$22,259 × (A/P,0.004375,72)
Calculating the interest factor;
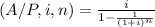
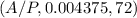 =
=
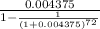 = 0.0162212
= 0.0162212
So,
Monthly installment=$22259 × 0.0162212= $361.0677
Now let us calculate the balance after 44th payment
B(44)= [$22,259 × (F/P,0.004375,44)] - [$361.0677 × (F/A,0.004375,44) ]
Calculating the interest factor;
(F/P,0.004375,44) =
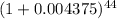 = 1.2117676
= 1.2117676
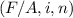 =
=
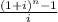
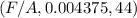 =
=
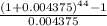 = 48.4040257
= 48.4040257
So,
B(44)= [$22,259 × 1.2117676] - [$361.0677 × 48.4040257] = $9495.6532
So, interest for 45th payment = I(45) = Balance due × Monthly interest rate
=9495.6532 ×0.004375
= $41.54
Principal associated with 45th payment=Monthly installment-Interest payment
=$361.0667 - $41.5435
= $319.5232
≅$319.52