Answer:
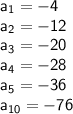
Explanation:
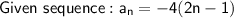
This formula is for the nth term of the sequence.
Therefore, to find any term of the sequence, substitute the position of the term you wish to find as n.
For example, to find the 10th term, substitute n = 10 into the formula:
![\begin{aligned}\sf a_(10) & =-4[2(10)-1)]\\ & = -4(20-1)\\ & = -4(19)\\ & = -76\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/high-school/gpoikln1v8xmjbtyh5zmy51uckhg7b3s8g.png)
To find the first 5 terms, substitute n = 1 through n = 5 into the formula:
![\sf a_1=-4[2(1)-1]=-4(2-1)=-4(1)=-4](https://img.qammunity.org/2023/formulas/mathematics/high-school/9ufhjha56rxksv0uwrgz01us8xjeme38kx.png)
![\sf a_2=-4[2(2)-1]=-4(4-1)=-4(3)=-12](https://img.qammunity.org/2023/formulas/mathematics/high-school/6h4h27kk6awh89yivmmobttcs2pqtlw1fw.png)
![\sf a_3=-4[2(3)-1]=-4(6-1)=-4(5)=-20](https://img.qammunity.org/2023/formulas/mathematics/high-school/3oxdyiuzrx687xs2fpetkpe7csucjfbz3m.png)
![\sf a_4=-4[2(4)-1]=-4(8-1)=-4(7)=-28](https://img.qammunity.org/2023/formulas/mathematics/high-school/yjjmojaljwl5a8wsxn7mm6uw6htmauan95.png)
![\sf a_5=-4[2(5)-1]=-4(10-1)=-4(9)=-36](https://img.qammunity.org/2023/formulas/mathematics/high-school/1i5bo9gobbqzyftxx9ntrqe8127pux2bqf.png)