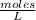Question

A student has two solutions of a substance. Solution-1: 25M, 400mL, and Solution-2: 30M, 300 ml. What is the molarity of the final solutions if these two solutions are mixed?

Answer 1

The molarity of the final solutions if these two solutions are mixed is 27.14
`(moles)/(L)`

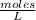
Step-by-step explanation:

Yo know:

• Solution-1: 25M, 400mL
• Solution-2: 30M, 300 mL

Molarity being the number of moles of solute per liter of solution, expressed by:

`Molarity (M)= (number of moles)/(volume)`

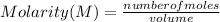
You can determine the number of moles that are mixed from each solution as:

Number of moles= Molarity*Volume

So, being 1 L=1000 mL, for each solution you get:

• Solution-1: being 0.400 L=400 mL ⇒ 25 M* 0.400 L= 10 moles
• Solution-2: being 0.300 L=300 mL ⇒ 30 M* 0.300 L= 9 moles

When mixing both solutions, it is obtained that the volume is the sum of both solutions:

Total volume= volume solution-1 + volume solution-2

and the number of total moles will be the sum of the moles of solution-1 and solution-2:

Total moles= moles of solution-1 + moles of solution-2

So the molarity of the final solution is:

`Molarity (M)= (moles of solution 1 + moles of solution 2)/(Volume solution 1 + Volume solution 2)`

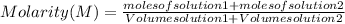
In this case, you have:

• moles of solution-1: 10 moles
• moles of solution-2: 9 moles
• volume solution-1: 0.400 L
• volume solution-2: 0.300 L

Replacing:

`Molarity (M)=(10 moles + 9 moles)/(0.400 L + 0.300 L)`

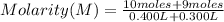
Solving:

`Molarity (M)=(19 moles)/(0.700 L)`

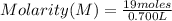
Molarity= 27.14
`(moles)/(L)`

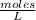
The molarity of the final solutions if these two solutions are mixed is 27.14
`(moles)/(L)`