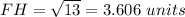Question

FH is the altitude to the hypotenuse EG. what is the length of FH. Really need some help with this!

Answer 1

Option A is correct

Explanation:

Given: FH is the altitude to the hypotenuse EG

To find: length of FH

Solution:

According to Pythagoras theorem, square of hypotenuse is equal to sum of squares of other two sides.

In
`\Delta EHF`,

`\angle EHF=90^(\circ)`

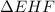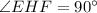
So,

`EF^2=EH^2+FH^2`

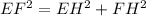
Put EH = 6 units and EF = 7 units

`7^2=6^2+FH^2\\49=36+FH^2\\49-36=FH^2\\13=FH^2`

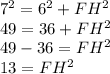
Option A is correct

Take square root on both sides

`FH=√(13)=3.606\,\,units`