Answer:
Explanation:
Before we begin this, there are a few things that need to be said and a few formulas you need to know. First is that we need to use the work form of a parabola, which is

All of the parabolas listed in blue highlight open either up or down, and this work form represents those 2 options. The only thing we need to know is that if there is a negative sign in front of the a, the parabola opens upside down like a mountain instead of up like a cup.
Another thing we need to know is how to find the focus of the parabola. The formula to find the focus for an "up" parabola is (h, k + p) and the formula to find the focus for an upside down parabola is (h, k - p). Then of course is the issue on how to find the p. p is found from the a in the above work form parabola, where
 .
.
In order to accomplish what we need to accomplish, we need to put each of those parabolas into work form (as previously stated) by completing the square. I'm hoping that since you are in pre-calculus you have already learned how to complete the square on a polynomial in order to factor it. Starting with the first one, we will complete the square. I'll go through each step one at a time, but will provide no explanation as to how I got there (again, assuming you know how to complete the square).
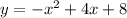 and, completing the square one step at a time:
and, completing the square one step at a time:
 and
and
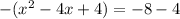 and
and
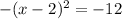 and
and
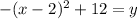
From this we can see that the h and k values for the vertex are h = 2 and k = 12. Now to find p.
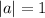 , ∴
, ∴
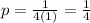
Using the correct focus formula (h, k - p), we get that the focus is
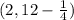 which simplifies to (2, 11.75) which is choice 2 in your options.
which simplifies to (2, 11.75) which is choice 2 in your options.
Now for the second one (yes, this takes forever...)
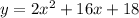 and completing the square one step at a time:
and completing the square one step at a time:
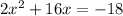 and
and
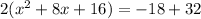 and
and
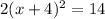 and
and
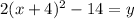
From this we can see that the vertex is h = -4 and k = -14. Now to find p from a.
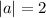 , ∴
, ∴
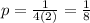 .
.
Using the correct focus formula for an upwards opening parabola (h, k + p),
 which simplifies down to (-4, -13.875) which is choice 3 in your options.
which simplifies down to (-4, -13.875) which is choice 3 in your options.
Now for the third one...
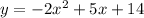 and completing the square step by step:
and completing the square step by step:
 and
and
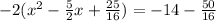 and
and
 and
and
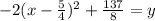
From that we can see the vertex values h and k. h = 1.25 and k = 17.125. Now to find p.
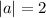 , ∴
, ∴
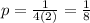
Using the correct focus formula for an upside down parabola (h, k - p),
 which simplifies down to (1.25, 17) which is choice 4 in your options.
which simplifies down to (1.25, 17) which is choice 4 in your options.
Now for the fourth one...
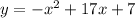 and completing the square step by step:
and completing the square step by step:
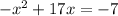 and
and
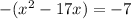 and
and
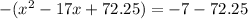 and
and
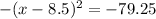 and
and
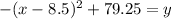
From that we see that the vertex is h = 8.5 and k = 79.25. Now to find p.
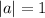 , ∴
, ∴
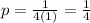
Using the correct formula for an upside down parabola (h, k - p),
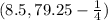 which simplifies down to (8.5, 79) and I don't see a choice from your available options there.
which simplifies down to (8.5, 79) and I don't see a choice from your available options there.
On to the fifth one...
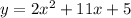 and again step by step:
and again step by step:
 and
and
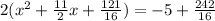 and
and
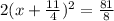 and
and
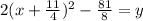
from which we see that h = -2.75 and k = -10.125. Now for p.
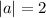 , ∴
, ∴
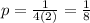
Using the correct focus formula for an upwards opening parabola (h, k + p),
 which simplifies down to (-2.75, -10) which is choice 1 from your options.
which simplifies down to (-2.75, -10) which is choice 1 from your options.
Now for the last one (almost there!):
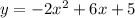 and
and
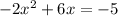 and
and
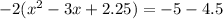 and
and
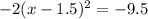 and
and
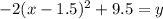
from which we see that h = 1.5 and k = 9.5. Now for p.
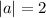 , ∴
, ∴
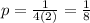
Using the formula for the focus of an upside down parabola (h, k - p),
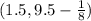 which simplifies down to (1.5, 9.375) which is another one I do not see in your choices.
which simplifies down to (1.5, 9.375) which is another one I do not see in your choices.
Good luck with your conic sections!!!