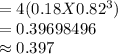Question

Consider the experiment of flipping a coin 4 times where the probability of flipping a heads is 0.18. So each outcome of the experiment would be a string of heads and tails of length 4. Assuming each flip is independent, what is the probability that there is a single heads out of the 4 flips?

Solution is given as .397 - how is this solution obtained?

Answer 1

0.397

Explanation:

In the experiment, if the coin is flipped 4 times, the outcomes in which there is a single heads out of the 4 flips are:

HTTT,THTT,TTHT and TTTH

The probability of flipping a head, P(Head)=0.18

Therefore: The probability of flipping a tail, P(Tail)=1-0.18=0.82

We can then calculate the probability that there is a single heads out of the 4 flips

=P(HTTT)+P(THTT)+P(TTHT)+P(TTTH)

=(0.18 X 0.82 X 0.82 X 0.82) + (0.82 X 0.18 X 0.82 X 0.82) + (0.82 X 0.82 X 0.18 X 0.82 )+ (0.82 X 0.82 X 0.82 X 0.18)

`=4(0.18X0.82^3)\\=0.39698496\\\approx 0.397`