Question

The volume of a stock is the number of shares traded for a given day. Several years​ ago, a certain​ company's stock had a mean daily volume of 7.52 million​ shares, according to a reputable financial news outlet. A random sample of 40 trading days in a recent year was obtained and the volume of shares traded on those days was​ recorded, with the accompanying results.

Required:
a. Find the test statistic:
b. Find the P-value
c. The level of significance is .05. what can be concluded from the hypothesis?


Volume (millions of shares)

4.1531 2.8893
4.6228 6.0203
5.6386 6.2774
4.5822 3.968
5.6903 4.0065
4.4313 11.2343
7.3941 2.6991
9.0557 3.2285
7 9800 4.2762
10.1556 3.2913
3.4189 5.8544
4.5624 2.6153
7.3287 8.1435
9.1723 5.3304
3.6798 4.1807
4.2868 5.3668
5.5448 1.7945
3.7656 5.0502
4.0201 3.1832
3 .798 5.4563

Answer 1

a) test statistic,
`t_(s) = -4.20`

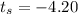
b) P-value = 0.0001

c) It can be concluded from the hypothesis that the company's stock has a mean value that is not 7.52 million shares i.e. the mean stock has changed in recent years

Explanation:

There are 40 trading days, therefore, sample size, n = 40

Calculate the Sample mean:

`\bar x = (\sum x)/(n) \\\bar x = (4.153 +4.6228 + ...+...+5.4563)/(40)\\\bar x = 5.5945`

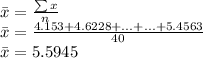
Get the null and alternative hypothesis:

Null hypothesis,
`H_(0) : \mu = 7.52`

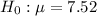
Alternative hypothesis,
`H_(a) : \mu \\eq 7.52`

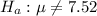
Calculate the sample standard deviation:

`SD = \sqrt{(\sum (x - \bar x)^(2) )/(n - 1) } \\SD = \sqrt{((4.1531-5.5945)^(2) + (4.6228-5.5945)^(2)+...+ (5.4563-5.5945)^(2))/(39) } \\SD = \sqrt{(327.6161)/(39) } \\SD = 2.8983`

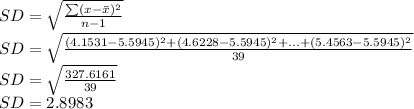
a) Calculate the test statistic:

`t_(s) = \frac{\bar{x} - \mu}{SD/√(n) } \\t_(s) = (5.5945 -7.52)/(2.8983/√(40) )\\t_(s) = -4.20`

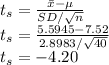
b) Calculate the P-value

Getting the P-value using the excel function:

P-value = (=T.DIST.2T(|ts|, df))

P-value = (=T.DIST.2T(4.20, 39))

P-value = 0.0001

c) If the level of significance,
`\alpha = 0.05`

The P-value (0.0001) < α(0.05), the null hypothesis is rejected.

It can therefore be concluded from the hypothesis that the company's stock has a mean value that is not 7.52 million shares i.e. the mean stock has changed in recent years