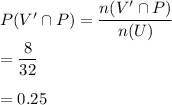Answer:
(a)9
(b)I. 0.28125
II. 0.46875
III. 0.25
Explanation:
There are a total of 32 students, therefore the number of elements in the Universal set, n(U)=32
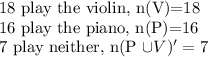
(a)The Venn diagram is attached below.
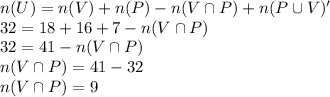
Therefore, 9 students play both the violin and piano.
(b)
I. Probability that the student plays the violin but not the piano
Number of Students who play violin only =18-x=18-9=9
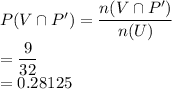
ii.Probability that the student does not play the violin
Number of Students who does not play violin only =17-x+7=17-9+7=15
P(does not play violin only)
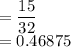
iii.Probability that the student plays the piano but not the violin
Number of Students who play piano only =17-x=17-9=8