Question

Suppose researchers conducted a study to see if the mean body temperature for adults was different from 98.6 degrees Fahrenheit. For this study, they took a random sample of 25 healthy adults and found a mean body temperature of 98.2 degrees Fahrenheit for the sample with a standard deviation of 0.6 degrees. The temperatures of the sample participants were unimodal and symmetric.

a. Write the null hypothesis and alternative hypothesis and define your parameter.
b. Show that the necessary conditions (Randomization Condition, 10% Condition, Nearly Normal Condition) are satisfied to perform a hypothesis test. Briefly explain how each condition is satisfied.
c. Perform the hypothesis test and find the P-value. (To show your work: Write down which calculator you are using and what values you are entering into the calculator.)
d. Is there strong evidence that the mean body temperature is different than 98.6 degrees? Briefly explain how you know.

Answer 1

a. As this is a one-sample two-tailed t-test for the mean, the null and alternative hypothesis are:

`H_0: \mu=98.6\\\\H_a:\mu\\eq 98.6`

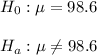
b. Conditions:

Randomization condition: the sample is selected randomly.

10% condition: the sample represents less than 10% of the population.

Nearly normal condition: the temperature is unimodal and symmetrical, so it can be approximated to a normal distribution.

c. In the step-by-step explanation.

d. There is strong evidence (signficance level α=0.05) to support the claim that the mean body temperature for adults is significantly different from 98.6 degrees Fahrenheit.

The P-value (P=0.003) shows that a sample result like this has very low prorbability if the null hypothesis is true, so it allows to think that the null hypothesis is not really correct.

Explanation:

This is a hypothesis test for the population mean.

The claim is that the mean body temperature for adults is significantly different from 98.6 degrees Fahrenheit. So this is a two-tailed test.

Then, the null and alternative hypothesis are:

`H_0: \mu=98.6\\\\H_a:\mu\\eq 98.6`

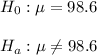
The significance level is assumed to be 0.05.

The sample has a size n=25.

The sample mean is M=98.2.

As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=0.6.

The estimated standard error of the mean is computed using the formula:

`s_M=(s)/(√(n))=(0.6)/(√(25))=0.12`

Then, we can calculate the t-statistic as:

`t=(M-\mu)/(s/√(n))=(98.2-98.6)/(0.12)=(-0.4)/(0.12)=-3.33`

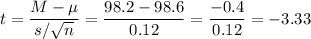
The degrees of freedom for this sample size are:

`df=n-1=25-1=24`

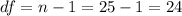
This test is a two-tailed test, with 24 degrees of freedom and t=-3.33, so the P-value for this test is calculated as (using a t-table):

`P-value=2\cdot P(t<-3.33)=0.003`

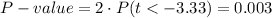
As the P-value (0.003) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is strong evidence (signficance level α=0.05) to support the claim that the mean body temperature for adults is significantly different from 98.6 degrees Fahrenheit.