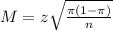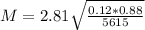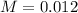Answer:
a) A sample size of 5615 is needed.
b) 0.012
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:
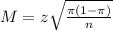
99.5% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
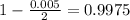 , so
, so
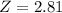 .
.
(a) Past studies suggest that this proportion will be about 0.2. Find the sample size needed if the margin of the error of the confidence interval is to be about 0.015.
This is n for which M = 0.015.
We have that
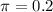
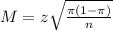

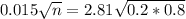
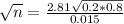
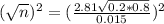
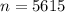
A sample size of 5615 is needed.
(b) Using the sample size above, when the sample is actually contacted, 12% of the sample say they are not satisfied. What is the margin of the error of the confidence interval?
Now
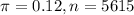 .
.
We have to find M.