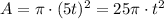Answer:
a)
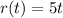
b)
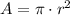
c)
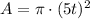
d)
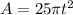
Explanation:
We know that the circle is increasing its radio from an initial state of r=0 cm, at a rate of 5 cm/s.
This can be expressed as:

a) Radius of the circle, r (in cm), in terms of the number of seconds, t since the circle started growing:
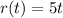
b) Area of the circle, A (in square cm), in terms of the circle's radius, r (in cm):
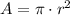
c) Circle's area, A (in square cm), in terms of the number of seconds, t, since the circle started growing:
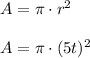
d) Expanded form for the area A: