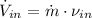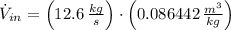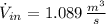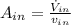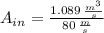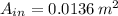Answer:
a)
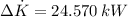 , b)
, b)
 , c)
, c)
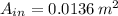
Step-by-step explanation:
A turbine is a device which works usually in steady state and assumption of being adiabatic means no heat interactions between steam through turbine and surroudings and produce mechanical work from fluid energy. Changes in gravitational energy can be neglected. This system can be modelled after the First Law of Thermodynamics:
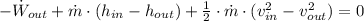
a) Change in kinetic energy
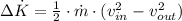
![\Delta \dot K = (1)/(2) \cdot \left(12.6\,(kg)/(s) \right) \cdot \left[\left(80\,(m)/(s) \right)^(2)-\left(50\,(m)/(s) \right)^(2)\right]](https://img.qammunity.org/2021/formulas/physics/college/athl1v2nsfsqumm7g8ytg9258kzp9xh9yu.png)

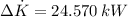
b) Power output
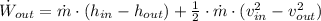


c) Turbine inlet area
Turbine inlet area can be found by using the following expressions: