Question

Determine whether each of the following sequences are arithmetic, geometric or neither. If arithmetic, state the common difference. If geometric, state the common ratio. -29, -34, -39, -44, -49, ...

Is this: common difference =5?
arithmetic?

Answer 1

`\qquad\qquad\huge\underline{{\sf Answer}}`

`\textbf{Let's see if the sequence is Arithmetic :}`

`\textsf{If the difference between successive terms is }`
`\textsf{equal then, the terms are in AP}`

• 
  `\textsf{-34 - (-29) = -5 }`

• 
  `\textsf{-39 - (-34) = -5 }`

`\textsf{Since the common difference is same, }`
`\textsf{we can infer that it's an Arithmetic progression}`
`\textsf{with common difference of -5}`

Answer 2

Sequence: -29, -34, -39, -44, -49, ...

First we need to identify the terms:

• 1st term = -29

• 2nd term = -34

• 3rd term = -39

• 4th term = -44

• 5th term = -49

If the sequence is arithmetic,
`\boxed{\sf \bold{second \ term = (first \ term+third \ term)/(2) }}`

If the sequence is geometric,
`\boxed{\sf \bold{second \ term = √(first \ term \ x \ third \ term) }}`

=======================================

Check for arithmetic

`\rightarrow \sf -34 = \sf (-29 +(-39))/(2)`

`\rightarrow \sf -34 = \sf (-68)/(2)`

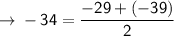
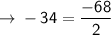
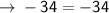`\rightarrow \sf -34 = -34` [Hence it's arithmetic series]

To find common difference. we have to think of how to go to next term.

first term: -29

to go the second term, subtract by -5

-29 -5 = -34, second term

-34 - 5 = -39, third term

Hence, common difference: -5

Solutions:

Arithmetic Sequence

Common Difference: -5